Quantum annealing (QA) is an optimization process for finding the global minimum of a given objective function over a given set of candidate solutions (candidate states), by a process using quantum fluctuations. Quantum annealing is used mainly for problems where the search space is discrete (combinatorial optimization problems) with many local minima; such as finding[1] the ground state of a spin glass or the traveling salesman problem. The term "quantum annealing" was first proposed in 1988 by B. Apolloni, N. Cesa Bianchi and D. De Falco as a quantum-inspired classical algorithm.[2][3] It was formulated in its present form by T. Kadowaki and H. Nishimori (ja) in 1998[4] though an imaginary-time variant without quantum coherence had been discussed by A. B. Finnila, M. A. Gomez, C. Sebenik and J. D. Doll in 1994.[5]
Quantum annealing starts from a quantum-mechanical superposition of all possible states (candidate states) with equal weights. Then the system evolves following the time-dependent Schrödinger equation, a natural quantum-mechanical evolution of physical systems. The amplitudes of all candidate states keep changing, realizing a quantum parallelism, according to the time-dependent strength of the transverse field, which causes quantum tunneling between states or essentially tunneling through peaks. If the rate of change of the transverse field is slow enough, the system stays close to the ground state of the instantaneous Hamiltonian (also see adiabatic quantum computation).[6] If the rate of change of the transverse field is accelerated, the system may leave the ground state temporarily but produce a higher likelihood of concluding in the ground state of the final problem Hamiltonian, i.e., diabatic quantum computation.[7][8] The transverse field is finally switched off, and the system is expected to have reached the ground state of the classical Ising model that corresponds to the solution to the original optimization problem. An experimental demonstration of the success of quantum annealing for random magnets was reported immediately after the initial theoretical proposal.[9] Quantum annealing has also been proven to provide a fast Grover oracle for the square-root speedup in solving many NP-complete problems.[10]
Comparison to Simulated Annealing
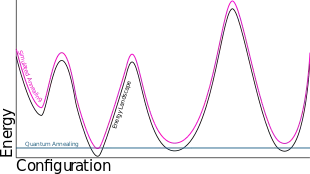
Quantum annealing can be compared to simulated annealing, whose "temperature" parameter plays a similar role to QA's tunneling field strength. In simulated annealing, the temperature determines the probability of moving to a state of higher "energy" from a single current state. In quantum annealing, the strength of transverse field determines the quantum-mechanical probability to change the amplitudes of all states in parallel. Analytical[11] and numerical[12] evidence suggests that quantum annealing outperforms simulated annealing under certain conditions (see[13] for a careful analysis, and,[14] for a fully solvable model of quantum annealing to arbitrary target Hamiltonian and comparison of different computation approaches).
Quantum mechanics: analogy and advantage
The tunneling field is basically a kinetic energy term that does not commute with the classical potential energy part of the original glass. The whole process can be simulated in a computer using quantum Monte Carlo (or other stochastic technique), and thus obtain a heuristic algorithm for finding the ground state of the classical glass.
In the case of annealing a purely mathematical objective function, one may consider the variables in the problem to be classical degrees of freedom, and the cost functions to be the potential energy function (classical Hamiltonian). Then a suitable term consisting of non-commuting variable(s) (i.e. variables that have non-zero commutator with the variables of the original mathematical problem) has to be introduced artificially in the Hamiltonian to play the role of the tunneling field (kinetic part). Then one may carry out the simulation with the quantum Hamiltonian thus constructed (the original function + non-commuting part) just as described above. Here, there is a choice in selecting the non-commuting term and the efficiency of annealing may depend on that.
It has been demonstrated experimentally as well as theoretically, that quantum annealing can indeed outperform thermal annealing (simulated annealing) in certain cases, especially where the potential energy (cost) landscape consists of very high but thin barriers surrounding shallow local minima.[15] Since thermal transition probabilities (proportional to , with the temperature and the Boltzmann constant) depend only on the height of the barriers, for very high barriers, it is extremely difficult for thermal fluctuations to get the system out from such local minima. However, as argued earlier in 1989 by Ray, Chakrabarti & Chakrabarti,[1] the quantum tunneling probability through the same barrier (considered in isolation) depends not only on the height of the barrier, but also on its width and is approximately given by , where is the tunneling field.[16] This additional handle through the width , in presence of quantum tunneling, can be of major help: If the barriers are thin enough (i.e. ), quantum fluctuations can surely bring the system out of the shallow local minima. For an -spin glass, the barrier height becomes of order . For constant value of one gets proportional to for the annealing time (instead of proportional to for thermal annealing), while can even become -independent for cases where decreases as .[17][18]
It is speculated that in a quantum computer, such simulations would be much more efficient and exact than that done in a classical computer, because it can perform the tunneling directly, rather than needing to add it by hand. Moreover, it may be able to do this without the tight error controls needed to harness the quantum entanglement used in more traditional quantum algorithms. Some confirmation of this is found in exactly solvable models.[19][20]
Timeline of ideas related to quantum annealing in Ising spin glasses:
- 1989 Idea was presented that quantum fluctuations could help explore rugged energy landscapes of the classical Ising spin glasses by escaping from local minima (having tall but thin barriers) using tunneling;[1]
- 1998 Formulation of quantum annealing and numerical test demonstrating its advantages in Ising glass systems;[4]
- 1999 First experimental demonstration of quantum annealing in LiHoYF Ising glass magnets;[21]
- 2011 Superconducting-circuit quantum annealing machine built and marketed by D-Wave Systems.[22]
D-Wave implementations

In 2011, D-Wave Systems announced the first commercial quantum annealer on the market by the name D-Wave One and published a paper in Nature on its performance.[22] The company claims this system uses a 128 qubit processor chipset.[23] On May 25, 2011, D-Wave announced that Lockheed Martin Corporation entered into an agreement to purchase a D-Wave One system.[24] On October 28, 2011 USC's Information Sciences Institute took delivery of Lockheed's D-Wave One.
In May 2013 it was announced that a consortium of Google, NASA Ames and the non-profit Universities Space Research Association purchased an adiabatic quantum computer from D-Wave Systems with 512 qubits.[25][26] An extensive study of its performance as quantum annealer, compared to some classical annealing algorithms, is already available.[27]
In June 2014, D-Wave announced a new quantum applications ecosystem with computational finance firm 1QB Information Technologies (1QBit) and cancer research group DNA-SEQ to focus on solving real-world problems with quantum hardware.[28] As the first company dedicated to producing software applications for commercially available quantum computers, 1QBit's research and development arm has focused on D-Wave's quantum annealing processors and has successfully demonstrated that these processors are suitable for solving real-world applications.[29]
With demonstrations of entanglement published,[30] the question of whether or not the D-Wave machine can demonstrate quantum speedup over all classical computers remains unanswered. A study published in Science in June 2014, described as "likely the most thorough and precise study that has been done on the performance of the D-Wave machine"[31] and "the fairest comparison yet", attempted to define and measure quantum speedup. Several definitions were put forward as some may be unverifiable by empirical tests, while others, though falsified, would nonetheless allow for the existence of performance advantages. The study found that the D-Wave chip "produced no quantum speedup" and did not rule out the possibility in future tests.[32] The researchers, led by Matthias Troyer at the Swiss Federal Institute of Technology, found "no quantum speedup" across the entire range of their tests, and only inconclusive results when looking at subsets of the tests. Their work illustrated "the subtle nature of the quantum speedup question". Further work[33] has advanced understanding of these test metrics and their reliance on equilibrated systems, thereby missing any signatures of advantage due to quantum dynamics.
There are many open questions regarding quantum speedup. The ETH reference in the previous section is just for one class of benchmark problems. Potentially there may be other classes of problems where quantum speedup might occur. Researchers at Google, LANL, USC, Texas A&M, and D-Wave are working to find such problem classes.[34]
In December 2015, Google announced that the D-Wave 2X outperforms both simulated annealing and Quantum Monte Carlo by up to a factor of 100,000,000 on a set of hard optimization problems.[35]
D-Wave's architecture differs from traditional quantum computers. It is not known to be polynomially equivalent to a universal quantum computer and, in particular, cannot execute Shor's algorithm because Shor's algorithm is not a hillclimbing process. Shor's algorithm requires a universal quantum computer. During the Qubits 2021 conference held by D-Wave, it was announced[36] that the company is hard at work developing their first universal quantum computers, capable of running Shor's algorithm in addition to other gate-model algorithms such as QAOA and VQE.
"A cross-disciplinary introduction to quantum annealing-based algorithms" [37] presents an introduction to combinatorial optimization (NP-hard) problems, the general structure of quantum annealing-based algorithms and two examples of this kind of algorithms for solving instances of the max-SAT and Minimum Multicut problems, together with an overview of the quantum annealing systems manufactured by D-Wave Systems. Hybrid quantum-classic algorithms for large-scale discrete-continuous optimization problems were reported to illustrate the quantum advantage.[38][39]
References
- 1 2 3 Ray, P.; Chakrabarti, B. K.; Chakrabarti, A. (1989). "Sherrington-Kirkpatrick model in a transverse field: Absence of replica symmetry breaking due to quantum fluctuations". Physical Review B. 39 (16): 11828–11832. Bibcode:1989PhRvB..3911828R. doi:10.1103/PhysRevB.39.11828. PMID 9948016.
- ↑ Apolloni, Bruno; Cesa-Bianchi, Nicolo; De Falco, Diego (July 1988). "A numerical implementation of quantum annealing". Stochastic Processes, Physics and Geometry, Proceedings of the Ascona-Locarno Conference.
- ↑ Apolloni, Bruno; Carvalho, Maria C.; De Falco, Diego (1989). "Quantum stochastic optimization". Stoc. Proc. Appl. 33 (2): 233–244. doi:10.1016/0304-4149(89)90040-9.
- 1 2 Kadowaki, T.; Nishimori, H. (1998). "Quantum annealing in the transverse Ising model". Phys. Rev. E. 58 (5): 5355. arXiv:cond-mat/9804280. Bibcode:1998PhRvE..58.5355K. doi:10.1103/PhysRevE.58.5355. S2CID 36114913. Archived from the original on 2013-08-11.
- ↑ Finnila, A.B.; Gomez, M.A.; Sebenik, C.; Stenson, C.; Doll, J.D. (1994). "Quantum annealing: A new method for minimizing multidimensional functions". Chemical Physics Letters. 219 (5–6): 343–348. arXiv:chem-ph/9404003. Bibcode:1994CPL...219..343F. doi:10.1016/0009-2614(94)00117-0. S2CID 97302385.
- ↑ Farhi, E.; Goldstone, J.; Gutmann, S.; Lapan, J.; Ludgren, A.; Preda, D. (2001). "A Quantum adiabatic evolution algorithm applied to random instances of an NP-Complete problem". Science. 292 (5516): 472–5. arXiv:quant-ph/0104129. Bibcode:2001Sci...292..472F. doi:10.1126/science.1057726. PMID 11313487. S2CID 10132718.
- ↑ Crosson, Elizabeth; Farhi, Edward; Cedric Yen-Yu Lin; Lin, Han-Hsuan; Shor, Peter (2014). "Different Strategies for Optimization Using the Quantum Adiabatic Algorithm". arXiv:1401.7320 [quant-ph].
- ↑ Muthukrishnan, Siddharth; Albash, Tameem; Lidar, Daniel A. (2015). "When Diabatic Trumps Adiabatic in Quantum Optimization". arXiv:1505.01249 [quant-ph].
- ↑ Brooke, J.; Bitko, D.; Rosenbaum, T. F.; Aeppli, G. (1999). "Quantum annealing of a disordered magnet". Science. 284 (5415): 779–81. arXiv:cond-mat/0105238. Bibcode:1999Sci...284..779B. doi:10.1126/science.284.5415.779. PMID 10221904. S2CID 37564720.
- ↑ Sinitsyn, N.; Yan, B. (2023). "Topologically protected Grover's oracle for the partition problem". Physical Review A. 108 (2): 022412. arXiv:2304.10488. Bibcode:2023PhRvA.108b2412S. doi:10.1103/PhysRevA.108.022412. S2CID 258236417.
- ↑ Morita, Satoshi; Nishimori, Hidetoshi (2008). "Mathematical foundation of quantum annealing". Journal of Mathematical Physics. 49 (12): 125210. arXiv:0806.1859. Bibcode:2008JMP....49l5210M. doi:10.1063/1.2995837. S2CID 13992889.
- ↑ Santoro, Giuseppe E. & Tosatti, Erio (18 August 2006). "Optimization using quantum mechanics: quantum annealing through adiabatic evolution". Journal of Physics A. 39 (36): R393–R431. Bibcode:2006JPhA...39R.393S. doi:10.1088/0305-4470/39/36/R01. S2CID 116931586.
- ↑ Heim, B.; Rønnow, T. F.; Isakov, S. V.; Troyer, M. (2015). "Quantum versus classical annealing of Ising spin glasses". Science. 348 (6231): 215–217. arXiv:1411.5693. Bibcode:2015Sci...348..215H. doi:10.1126/science.aaa4170. PMID 25765071.
- ↑ Yan, B.; Sinitsyn, N. A. (2022). "Analytical solution for nonadiabatic quantum annealing to arbitrary Ising spin Hamiltonian". Nature Communications. 13 (1): 2212. arXiv:2110.12354. Bibcode:2022NatCo..13.2212Y. doi:10.1038/s41467-022-29887-0. PMC 9038765. PMID 35468917. S2CID 248389790.
- ↑ "Local Maxima and Minima, and, Absolute Maxima and Minima". Mathonline.
- ↑ Das, A.; Chakrabarti, B. K. & Stinchcombe, R. B. (2005). "Quantum annealing in a kinetically constrained system". Phys. Rev. E. 72 (2): 026701. arXiv:cond-mat/0502167. Bibcode:2005PhRvE..72b6701D. doi:10.1103/PhysRevE.72.026701. PMID 16196745. S2CID 16466621. Archived from the original on 2014-01-13.
- ↑ See e.g., Mukherjee, S. & Chakrabarti, B. K. (2015). "Multivariable Optimization: Quantum Annealing & Computation". Eur. Phys. J. 224 (1): 17–24. arXiv:1408.3262. Bibcode:2015EPJST.224...17M. doi:10.1140/epjst/e2015-02339-y. S2CID 118525494.
- ↑ Das, A.; Chakrabarti, B. K. (2008). "Quantum Annealing and Analog Quantum Computation". Rev. Mod. Phys. 80 (3): 1061–1081. arXiv:0801.2193. Bibcode:2008RvMP...80.1061D. CiteSeerX 10.1.1.563.9990. doi:10.1103/RevModPhys.80.1061. S2CID 14255125.
- ↑ Li, F.; Chernyak, V. Y. & Sinitsyn, N. A. (2018). "Quantum annealing and thermalization: insights from integrability". Physical Review Letters. 121 (19): 190601. arXiv:1804.00371. Bibcode:2018arXiv180400371L. doi:10.1103/PhysRevLett.121.190601. PMID 30468584. S2CID 53594139.
- ↑ Yan, B.; Sinitsyn, N. A. (2022). "Analytical solution for nonadiabatic quantum annealing to arbitrary Ising spin Hamiltonian". Nature Communications. 13 (1): 2212. arXiv:2110.12354. Bibcode:2022NatCo..13.2212Y. doi:10.1038/s41467-022-29887-0. PMC 9038765. PMID 35468917. S2CID 248389790.
- ↑ Brooke, J.; Bitko, D.; Rosenbaum, T. F. & Aeppli, G. (30 April 1999). "Quantum Annealing of a Disordered Magnet". Science. 284 (5415): 779–781. arXiv:cond-mat/0105238. Bibcode:1999Sci...284..779B. doi:10.1126/science.284.5415.779. PMID 10221904. S2CID 37564720.
- 1 2 Johnson, M. W.; Amin, M. H. S.; Gildert, S.; et al. (2011). "Quantum annealing with manufactured spins". Nature. 473 (7346): 194–8. Bibcode:2011Natur.473..194J. doi:10.1038/nature10012. PMID 21562559. S2CID 205224761.
- ↑ "Learning to program the D-Wave One". D-Wave Systems blog. Archived from the original on July 23, 2011. Retrieved 11 May 2011.
- ↑ "D-Wave Systems sells its first Quantum Computing System to Lockheed Martin Corporation". D-Wave. 2011-05-25. Archived from the original on July 23, 2011. Retrieved 2011-05-30.
- ↑ Jones, N. (2013). "Google and NASA snap up quantum computer". Nature News. doi:10.1038/nature.2013.12999. S2CID 57405432.
- ↑ Smelyanskiy, Vadim N.; Rieffel, Eleanor G.; Knysh, Sergey I.; Williams, Colin P.; Johnson, Mark W.; Thom, Murray C.; Macready, William G.; Pudenz, Kristen L. (2012). "A Near-Term Quantum Computing Approach for Hard Computational Problems in Space Exploration". arXiv:1204.2821 [quant-ph].
- ↑ Boixo, S.; Rønnow, T. F.; Isakov, S. V.; Wang, Z.; Wecker, D.; Lidar, D. A.; Martinis, J. M.; Troyer, M. (2014). "Evidence for quantum annealing with more than one hundred qubits". Nature Physics. 10 (3): 218–224. arXiv:1304.4595. Bibcode:2014NatPh..10..218B. doi:10.1038/nphys2900. S2CID 8031023.
- ↑ "D-Wave Systems Building Quantum Application Ecosystem, Announces Partnerships with DNA-SEQ Alliance and 1QBit". D-Wave Systems. Archived from the original on 31 December 2019. Retrieved 22 June 2014.
- ↑ "1QBit Research". 1QBit. Archived from the original on 19 June 2014. Retrieved 22 June 2014.
- ↑ Lanting, T.; Przybysz, A. J.; Smirnov, A. Yu.; Spedalieri, F. M.; et al. (2014-05-29). "Entanglement in a quantum annealing processor". Physical Review X. 4 (2): 021041. arXiv:1401.3500. Bibcode:2014PhRvX...4b1041L. doi:10.1103/PhysRevX.4.021041. S2CID 19235104.
- ↑ Helmut Katzgraber, quoted in (Cho 2014).
- ↑ Cho, Adrian (20 June 2014). "Quantum or not, controversial computer yields no speedup". Science. 344 (6190): 1330–1331. Bibcode:2014Sci...344.1330C. doi:10.1126/science.344.6190.1330. PMID 24948715.
- ↑ Amin, Mohammad H. (2015). "Searching for quantum speedup in quasistatic quantum annealers". Physical Review A. 92 (5): 052323. arXiv:1503.04216. Bibcode:2015PhRvA..92e2323A. doi:10.1103/PhysRevA.92.052323. S2CID 66770023.
- ↑ Steiger, Damian; Heim, Bettina; Rønnow, Troels; Troyer, Matthias (October 22, 2015). "Performance of quantum annealing hardware". In Huckridge, David A.; Ebert, Reinhard; Gruneisen, Mark T.; Dusek, Miloslav; Rarity, John G. (eds.). Electro-Optical and Infrared Systems: Technology and Applications XII; and Quantum Information Science and Technology. Vol. 9648. p. 964816. Bibcode:2015SPIE.9648E..16S. doi:10.1117/12.2202661. S2CID 57916974.
- ↑ "When can Quantum Annealing win?". Research Blog. 8 December 2015. Retrieved 2016-01-21.
- ↑ D-Wave Systems (2021-10-05). "D-Wave's Next-Generation Roadmap: Bringing Clarity to Practical Quantum Computing". Medium. Retrieved 2021-11-12.
- ↑ Venegas-Andraca, Salvador E.; Cruz-Santos, William; McGeoch, Catherine; Lanzagorta, Marco (2018). "A cross-disciplinary introduction to quantum annealing-based algorithms". Contemporary Physics. 59 (2): 174–196. arXiv:1803.03372. Bibcode:2018ConPh..59..174V. doi:10.1080/00107514.2018.1450720. S2CID 118974781.
- ↑ Ajagekar, Akshay; Humble, Travis; You, Fengqi (2020-01-04). "Quantum computing based hybrid solution strategies for large-scale discrete-continuous optimization problems". Computers & Chemical Engineering. 132: 106630. arXiv:1910.13045. doi:10.1016/j.compchemeng.2019.106630. ISSN 0098-1354.
- ↑ Wierzbiński, M.; Falo-Roget, J.; Crimi, A. (2023). "Community detection in brain connectomes with hybrid quantum computing". Scientific Reports. 13 (1): 3446. Bibcode:2023NatSR..13.3446W. doi:10.1038/s41598-023-30579-y. PMC 9977923. PMID 36859591. S2CID 257236235.
Further reading
- Bapst, V.; Foini, L.; Krzakala, F.; Semerjian, G.; Zamponi, F. (2013). "The quantum adiabatic algorithm applied to random optimization problems: The quantum spin glass perspective". Physics Reports. 523 (3): 127–205. arXiv:1210.0811. Bibcode:2013PhR...523..127B. doi:10.1016/j.physrep.2012.10.002. S2CID 19019744.
- Chandra, Anjan K.; Das, Arnab & Chakrabarti, Bikas K., eds. (2010). Quantum Quenching, Annealing and Computation. Lecture Note in Physics. Vol. 802. Heidelberg: Springer. ISBN 978-3-64211-469-4.
- Das, Arnab & Chakrabarti, Bikas K., eds. (2005). Quantum Annealing and Related Optimization Methods. Lecture Note in Physics. Vol. 679. Heidelberg: Springer. ISBN 978-3-54027-987-7.
- Dutta, A.; Aeppli, G.; Chakrabarti, B. K.; Divakaran, U.; Rosenbaum, T.F. & Sen, D. (2015). Quantum Phase Transitions in Transverse Field Spin Models: From Statistical Physics to Quantum Information. Cambridge & Delhi: Cambridge University Press. ISBN 978-1-10706-879-7.
- Li, Fuxiang; Chernyak, V. Y.; Sinitsyn, N. A. (2013). "Quantum Annealing and Computation: A Brief Documentary Note". Science and Culture. 79: 485–500. arXiv:1310.1339. Bibcode:2013arXiv1310.1339G..
- Suzuki, S.; Inoue, J.-I. & Chakrabarti, B. K. (2013). "Chapter 8 on Quantum Annealing". Quantum Ising Phases & Transitions in Transverse Ising Models (2nd ed.). Heidelberg: Springer. ISBN 978-3-64233-038-4.
- Tanaka, S.; Tamura, R. & Chakrabarti, B. K. (2017). Quantum Spin Glasses, Annealing & Computation. Cambridge & Delhi: Cambridge University Press. ISBN 978-1-10711-319-0.
- "Quantum Annealing & Computation: Challenges & Perspectives". Philosophical Transactions A. Royal Society, London. 381. January 2023.