In mathematics, Pascal's rule (or Pascal's formula) is a combinatorial identity about binomial coefficients. It states that for positive natural numbers n and k,
where is a binomial coefficient; one interpretation of the coefficient of the xk term in the expansion of (1 + x)n. There is no restriction on the relative sizes of n and k,[1] since, if n < k the value of the binomial coefficient is zero and the identity remains valid.
Pascal's rule can also be viewed as a statement that the formula
solves the linear two-dimensional difference equation
over the natural numbers. Thus, Pascal's rule is also a statement about a formula for the numbers appearing in Pascal's triangle.
Pascal's rule can also be generalized to apply to multinomial coefficients.
Combinatorial proof
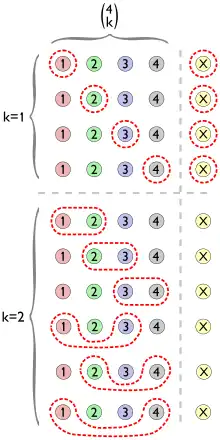
Pascal's rule has an intuitive combinatorial meaning, that is clearly expressed in this counting proof.[2]: 44
Proof. Recall that equals the number of subsets with k elements from a set with n elements. Suppose one particular element is uniquely labeled X in a set with n elements.
To construct a subset of k elements containing X, include X and choose k − 1 elements from the remaining n − 1 elements in the set. There are such subsets.
To construct a subset of k elements not containing X, choose k elements from the remaining n − 1 elements in the set. There are such subsets.
Every subset of k elements either contains X or not. The total number of subsets with k elements in a set of n elements is the sum of the number of subsets containing X and the number of subsets that do not contain X, .
This equals ; therefore, .
Algebraic proof
Alternatively, the algebraic derivation of the binomial case follows.
Generalization
Pascal's rule can be generalized to multinomial coefficients.[2]: 144 For any integer p such that , and ,
where is the coefficient of the term in the expansion of .
The algebraic derivation for this general case is as follows.[2]: 144 Let p be an integer such that , and . Then
See also
References
Bibliography
- Merris, Russell. Combinatorics. John Wiley & Sons. 2003 ISBN 978-0-471-26296-1
External links
This article incorporates material from Pascal's triangle on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
This article incorporates material from Pascal's rule proof on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.