In group theory, a branch of mathematics, an opposite group is a way to construct a group from another group that allows one to define right action as a special case of left action.
Monoids, groups, rings, and algebras can be viewed as categories with a single object. The construction of the opposite category generalizes the opposite group, opposite ring, etc.
Definition
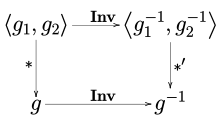
Let be a group under the operation . The opposite group of , denoted , has the same underlying set as , and its group operation is defined by .
If is abelian, then it is equal to its opposite group. Also, every group (not necessarily abelian) is naturally isomorphic to its opposite group: An isomorphism is given by . More generally, any antiautomorphism gives rise to a corresponding isomorphism via , since
Group action
Let be an object in some category, and be a right action. Then is a left action defined by , or .