| 8-cube Octeract | |
|---|---|
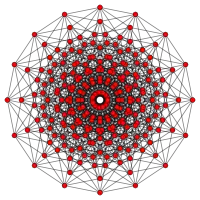
 Orthogonal projection inside Petrie polygon | |
| Type | Regular 8-polytope |
| Family | hypercube |
| Schläfli symbol | {4,36} |
| Coxeter-Dynkin diagrams |
|
| 7-faces | 16 {4,35} |
| 6-faces | 112 {4,34} |
| 5-faces | 448 {4,33} |
| 4-faces | 1120 {4,32} |
| Cells | 1792 {4,3} |
| Faces | 1792 {4} |
| Edges | 1024 |
| Vertices | 256 |
| Vertex figure | 7-simplex |
| Petrie polygon | hexadecagon |
| Coxeter group | C8, [36,4] |
| Dual | 8-orthoplex |
| Properties | convex, Hanner polytope |
In geometry, an 8-cube is an eight-dimensional hypercube. It has 256 vertices, 1024 edges, 1792 square faces, 1792 cubic cells, 1120 tesseract 4-faces, 448 5-cube 5-faces, 112 6-cube 6-faces, and 16 7-cube 7-faces.
It is represented by Schläfli symbol {4,36}, being composed of 3 7-cubes around each 6-face. It is called an octeract, a portmanteau of tesseract (the 4-cube) and oct for eight (dimensions) in Greek. It can also be called a regular hexdeca-8-tope or hexadecazetton, being an 8-dimensional polytope constructed from 16 regular facets.
It is a part of an infinite family of polytopes, called hypercubes. The dual of an 8-cube can be called an 8-orthoplex and is a part of the infinite family of cross-polytopes.
Cartesian coordinates
Cartesian coordinates for the vertices of an 8-cube centered at the origin and edge length 2 are
- (±1,±1,±1,±1,±1,±1,±1,±1)
while the interior of the same consists of all points (x0, x1, x2, x3, x4, x5, x6, x7) with -1 < xi < 1.
As a configuration
This configuration matrix represents the 8-cube. The rows and columns correspond to vertices, edges, faces, cells, 4-faces, 5-faces, 6-faces, and 7-faces. The diagonal numbers say how many of each element occur in the whole 8-cube. The nondiagonal numbers say how many of the column's element occur in or at the row's element.[1][2]
The diagonal f-vector numbers are derived through the Wythoff construction, dividing the full group order of a subgroup order by removing one mirror at a time.[3]
| B8 | k-face | fk | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | k-figure | notes | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A7 | ( ) | f0 | 256 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | {3,3,3,3,3,3} | B8/A7 = 2^8*8!/8! = 256 | |
| A6A1 | { } | f1 | 2 | 1024 | 7 | 21 | 35 | 35 | 21 | 7 | {3,3,3,3,3} | B8/A6A1 = 2^8*8!/7!/2 = 1024 | |
| A5B2 | {4} | f2 | 4 | 4 | 1792 | 6 | 15 | 20 | 15 | 6 | {3,3,3,3} | B8/A5B2 = 2^8*8!/6!/4/2 = 1792 | |
| A4B3 | {4,3} | f3 | 8 | 12 | 6 | 1792 | 5 | 10 | 10 | 5 | {3,3,3} | B8/A4B3 = 2^8*8!/5!/8/3! = 1792 | |
| A3B4 | {4,3,3} | f4 | 16 | 32 | 24 | 8 | 1120 | 4 | 6 | 4 | {3,3} | B8/A3B4 = 2^8*8!/4!/2^4/4! = 1120 | |
| A2B5 | {4,3,3,3} | f5 | 32 | 80 | 80 | 40 | 10 | 448 | 3 | 3 | {3} | B8/A2B5 = 2^8*8!/3!/2^5/5! = 448 | |
| A1B6 | {4,3,3,3,3} | f6 | 64 | 192 | 240 | 160 | 60 | 12 | 112 | 2 | { } | B8/A1B6 = 2^8*8!/2/2^6/6!= 112 | |
| B7 | {4,3,3,3,3,3} | f7 | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 16 | ( ) | B8/B7 = 2^8*8!/2^7/7! = 16 |
Projections
 This 8-cube graph is an orthogonal projection. This orientation shows columns of vertices positioned a vertex-edge-vertex distance from one vertex on the left to one vertex on the right, and edges attaching adjacent columns of vertices. The number of vertices in each column represents rows in Pascal's triangle, being 1:8:28:56:70:56:28:8:1. |
| B8 | B7 | ||||
|---|---|---|---|---|---|
 |
 | ||||
| [16] | [14] | ||||
| B6 | B5 | ||||
 |
 | ||||
| [12] | [10] | ||||
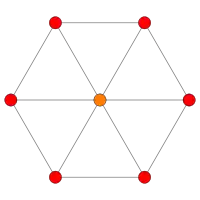
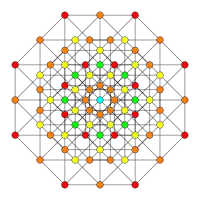
| B4 | B3 | B2 | |||
 |
 |
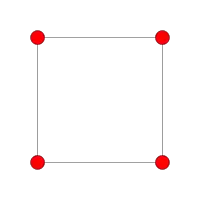 | |||
| [8] | [6] | [4] | |||
| A7 | A5 | A3 | |||
 |
 |
 | |||
| [8] | [6] | [4] | |||
Derived polytopes
Applying an alternation operation, deleting alternating vertices of the octeract, creates another uniform polytope, called a 8-demicube, (part of an infinite family called demihypercubes), which has 16 demihepteractic and 128 8-simplex facets.
Related polytopes
The 8-cube is 8th in an infinite series of hypercube:
 |
 |
 |
 |
 |
 |
 |
 |
| Line segment | Square | Cube | 4-cube | 5-cube | 6-cube | 7-cube | 8-cube |
References
- ↑ Coxeter, Regular Polytopes, sec 1.8 Configurations
- ↑ Coxeter, Complex Regular Polytopes, p.117
- ↑ Klitzing, Richard. "o3o3o3o3o3o3o4x - octo".
- H.S.M. Coxeter:
- Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- Klitzing, Richard. "8D uniform polytopes (polyzetta) o3o3o3o3o3o3o4x - octo".
External links
- Weisstein, Eric W. "Hypercube". MathWorld.
- Olshevsky, George. "Measure polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Multi-dimensional Glossary: hypercube Garrett Jones