
In signal processing, the Nyquist frequency (or folding frequency), named after Harry Nyquist, is a characteristic of a sampler, which converts a continuous function or signal into a discrete sequence. For a given sampling rate (samples per second), the Nyquist frequency (cycles per second) is the frequency whose cycle-length (or period) is twice the interval between samples, thus 0.5 cycle/sample. For example, audio CDs have a sampling rate of 44100 samples/second. At 0.5 cycle/sample, the corresponding Nyquist frequency is 22050 cycles/second (Hz). Conversely, the Nyquist rate for sampling a 22050 Hz signal is 44100 samples/second.[1][2][upper-alpha 1]
When the highest frequency (bandwidth) of a signal is less than the Nyquist frequency of the sampler, the resulting discrete-time sequence is said to be free of the distortion known as aliasing, and the corresponding sample rate is said to be above the Nyquist rate for that particular signal.[3][4]
In a typical application of sampling, one first chooses the highest frequency to be preserved and recreated, based on the expected content (voice, music, etc.) and desired fidelity. Then one inserts an anti-aliasing filter ahead of the sampler. Its job is to attenuate the frequencies above that limit. Finally, based on the characteristics of the filter, one chooses a sample rate (and corresponding Nyquist frequency) that will provide an acceptably small amount of aliasing. In applications where the sample rate is pre-determined (such as the CD rate), the filter is chosen based on the Nyquist frequency, rather than vice versa.
Folding frequency
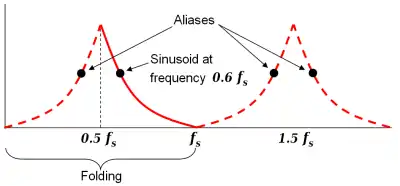
In this example, fs is the sampling rate, and 0.5 cycle/sample × fs is the corresponding Nyquist frequency. The black dot plotted at 0.6 fs represents the amplitude and frequency of a sinusoidal function whose frequency is 60% of the sample rate. The other three dots indicate the frequencies and amplitudes of three other sinusoids that would produce the same set of samples as the actual sinusoid that was sampled. Undersampling of the sinusoid at 0.6 fs is what allows there to be a lower-frequency alias. If the true frequency were 0.4 fs, there would still be aliases at 0.6, 1.4, 1.6, etc.
The red lines depict the paths (loci) of the 4 dots if we were to adjust the frequency and amplitude of the sinusoid along the solid red segment (between fs/2 and fs). No matter what function we choose to change the amplitude vs frequency, the graph will exhibit symmetry between 0 and fs. This symmetry is commonly referred to as folding, and another name for fs/2 (the Nyquist frequency) is folding frequency.[5]
Other meanings
Early uses of the term Nyquist frequency, such as those cited above, are all consistent with the definition presented in this article. Some later publications, including some respectable textbooks, call twice the signal bandwidth the Nyquist frequency;[6][7] this is a distinctly minority usage, and the frequency at twice the signal bandwidth is otherwise commonly referred to as the Nyquist rate.
Notes
- ↑ When the function domain is distance, as in an image sampling system, the sample rate might be dots per inch and the corresponding Nyquist frequency would be in cycles per inch.
References
- ↑
Grenander, Ulf (1959). Probability and Statistics: The Harald Cramér Volume. Wiley.
The Nyquist frequency is that frequency whose period is two sampling intervals.
- ↑
John W. Leis (2011). Digital Signal Processing Using MATLAB for Students and Researchers. John Wiley & Sons. p. 82. ISBN 9781118033807.
The Nyquist rate is twice the bandwidth of the signal ... The Nyquist frequency or folding frequency is half the sampling rate and corresponds to the highest frequency which a sampled data system can reproduce without error.
- ↑ James J. Condon & Scott M. Ransom (2016). Essential Radio Astronomy. Princeton University Press. pp. 280–281. ISBN 9781400881161.
- ↑
Harry L. Stiltz (1961). Aerospace Telemetry. Prentice-Hall. ISBN 9780130182838.
the existence of power in the continuous signal spectrum at frequencies higher than the Nyquist frequency is the cause of aliasing error
- ↑
Thomas Zawistowski; Paras Shah. "An Introduction to Sampling Theory". Retrieved 17 April 2010.
Frequencies "fold" around half the sampling frequency - which is why the [Nyquist] frequency is often referred to as the folding frequency.
- ↑ Jonathan M. Blackledge (2003). Digital Signal Processing: Mathematical and Computational Methods, Software Development and Applications. Horwood Publishing. ISBN 1-898563-48-9.
- ↑
Paulo Sergio Ramirez Diniz, Eduardo A. B. Da Silva, Sergio L. Netto (2002). Digital Signal Processing: System Analysis and Design. Cambridge University Press. ISBN 0-521-78175-2.
{{cite book}}: CS1 maint: multiple names: authors list (link)