
| 1. | One Sonobe module | |
|---|---|---|
| 3. | Opened (left) and completed (right) Toshie's Jewel (triangular bipyramid) | |
| 6. | Cube (triakis tetrahedron) | |
| 12. | Triakis octahedron | |
| 30. | Triakis icosahedron |
The Sonobe module is one of the many units used to build modular origami. The popularity of Sonobe modular origami models derives from the simplicity of folding the modules, the sturdy and easy assembly, and the flexibility of the system.
History
The origin of the Sonobe module is unknown. Two possible creators are Toshie Takahama and Mitsunobu Sonobe, who published several books together and both members of Sosaku Origami Group 67. The earliest appearance of a Sonobe module was in a cube attributed to Mitsunobu Sonobe in a Sosaku Origami Group book published in 1968, however it does not reveal whether he invented the module or used an earlier design: the phrase "finished model by Mitsunobu Sonobe" is ambiguous. Its next appearance was "Toshie's Jewel", which appeared in 1974. However neither folder took advantage of the full potential of the module. This potential was discovered in the 1970s by other folders – particularly Steve Krimball, who created the 30-unit ball – as part of a sudden period of development in modular origami. Despite the module's importance and continued popularity, its designer remains uncertain.[2]
Description
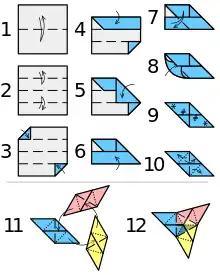
Each individual unit is folded from a square sheet of paper, of which only one face is visible in the finished module; many ornamented variants of the plain Sonobe unit that expose both sides of the paper have been designed.
The Sonobe unit has the shape of a parallelogram with 45 and 135 degrees angles, divided by creases into two diagonal tabs at the ends and two corresponding pockets within the inscribed center square. The system can build a wide range of three-dimensional geometric forms by docking these tabs into the pockets of adjacent units. Three interconnected Sonobe units will form an open-bottomed triangular pyramid with an equilateral triangle for the open bottom, and isosceles right triangles as the other three faces. It will have a right-angle apex (equivalent to the corner of a cube) and three tab/pocket flaps protruding from the base. This particularly suits polyhedra that have equilateral triangular faces: Sonobe modules can replace each notional edge of the original deltahedron by the central diagonal fold of one unit and each equilateral triangle with a right-angle pyramid consisting of one half each of three units, without dangling flaps. The pyramids can be made to point inwards; assembly is more difficult but some cases of encroaching can be obviously prevented.
The simplest shape made of these pyramids, often called "Toshie's Jewel" (shown above), is named after origami enthusiast Toshie Takahama. It is a three-unit hexahedron built around the notional scaffold of a flat equilateral triangle (two "faces", three edges); the protruding tab/pocket flaps are simply reconnected on the underside, resulting in two triangular pyramids joined at the base, a triangular bipyramid.
The most popular intermediate model is the triakis icosahedron, shown below. It requires 30 units to build.
Usage


The table below shows the correlation between three basic characteristics – faces, edges, and vertices – of polygons (composed of Toshie's Jewel sub-units) of varying size and the number of Sonobe units used:
| Number of Sonobe Units | Faces | Edges | Vertices |
|---|---|---|---|
| s | 2s | 3s | s + 2 |
| 3 | 6 | 9 | 5 |
| 6 | 12 | 18 | 8 |
| 12 | 24 | 36 | 14 |
| 30 | 60 | 90 | 32 |
| 90 | 180 | 270 | 92 |
| 120 | 240 | 360 | 122 |
| 270 | 540 | 810 | 272 |
The model made of three units results in a triangular bipyramid. Building a pyramid on each face of a regular tetrahedron, using six units, results in a cube (the central fold of each module lays flat, creating square faces instead of isosceles right triangular faces, and changing the formula for the number of faces, edges, and vertices), or triakis tetrahedron. Building a pyramid on each face of a regular octahedron, using twelve Sonobe units, results in a triakis octahedron. Building a pyramid on each face of a regular icosahedron requires 30 units, and results in a triakis icosahedron.
Uniform polyhedra can be adapted to Sonobe modules by replacing non-triangular faces with pyramids having equilateral faces; for example by adding pentagonal pyramids pointing inwards to the faces of a dodecahedron a 90-module ball can be obtained.
The 270-module ball looks like a very complicated shape, but it is just an icosahedron with each triangular face divided into 9 small triangles. Each small triangle is made of 3 sonobe units.
Arbitrary shapes, beyond symmetrical polyhedra, can also be constructed; a deltahedron with 2N faces and 3N edges requires 3N Sonobe modules. A popular class of arbitrary shapes consists of assemblies of equal size cubes in a regular cubic grid, which can be easily derived from the six unit cube by joining multiple ones at faces or edges.
There are two popular variants of the main assembly style of three modules in triangular pyramids, both using the same flaps and pockets and compatible with it:
- Joining four modules together (instead of three), forming a flattened square pyramid that can become part of a quilt or a larger polyhedral face, e.g. in 12 and 24 modules large cubes. Such a square lacks structural integrity because without the diagonal folds the flaps are not restrained to stay in the far corner of the pockets.
- Joining only two modules, forming a triangular fin that can be used as an ornament for suitable models and to make a 1 module triangle (one fin, made with the two halves of the same module) or a 2 module square (two fins).
Notes and references
Bibliography
- Takahama, Toshie, and Kunihiko Kasahara. Origami for the Connoisseur. Japan Publications, Tokyo, 1987. ISBN 4-8170-9002-2
- Takahama, Toshie, "Creative Life with Creative Origami" Volume I (1974) (original source for Toshie's jewel)
- Sosaku Origami Group 67, Magazine 2 (Mitsunobu's original cube)