In cryptography, ciphertext stealing (CTS) is a general method of using a block cipher mode of operation that allows for processing of messages that are not evenly divisible into blocks without resulting in any expansion of the ciphertext, at the cost of slightly increased complexity.
General characteristics
Ciphertext stealing is a technique for encrypting plaintext using a block cipher, without padding the message to a multiple of the block size, so the ciphertext is the same size as the plaintext.
It does this by altering processing of the last two blocks of the message. The processing of all but the last two blocks is unchanged, but a portion of the second-to-last block's ciphertext is "stolen" to pad the last plaintext block. The padded final block is then encrypted as usual.
The final ciphertext, for the last two blocks, consists of the partial penultimate block (with the "stolen" portion omitted) plus the full final block, which are the same size as the original plaintext.
Decryption requires decrypting the final block first, then restoring the stolen ciphertext to the penultimate block, which can then be decrypted as usual.
In principle any block-oriented block cipher mode of operation can be used, but stream-cipher-like modes can already be applied to messages of arbitrary length without padding, so they do not benefit from this technique. The common modes of operation that are coupled with ciphertext stealing are Electronic Codebook (ECB) and Cipher Block Chaining (CBC).
Ciphertext stealing for ECB mode requires the plaintext to be longer than one block. A possible workaround is to use a stream cipher-like block cipher mode of operation when the plaintext length is one block or less, such as the CTR, CFB or OFB modes.
Ciphertext stealing for CBC mode doesn't necessarily require the plaintext to be longer than one block. In the case where the plaintext is one block long or less, the Initialization vector (IV) can act as the prior block of ciphertext. In this case a modified IV must be sent to the receiver. This may not be possible in situations where the IV can not be freely chosen by the sender when the ciphertext is sent (e.g., when the IV is a derived or pre-established value), and in this case ciphertext stealing for CBC mode can only occur in plaintexts longer than one block.
To implement CTS encryption or decryption for data of unknown length, the implementation must delay processing (and buffer) the two most recent blocks of data, so that they can be properly processed at the end of the data stream.
Ciphertext format
There are several different ways to arrange the ciphertext for transmission. The ciphertext bits are the same in all cases, just transmitted in a different order, so the choice has no security implications; it is purely one of implementation convenience.
The numbering here is taken from Dworkin, who describes them all. The third is the most popular, and described by Daemen and Schneier; Meyer describes a related, but incompatible scheme (with respect to bit ordering and key use).
CS1
Arguably the most obvious way to arrange the ciphertext is to transmit the truncated penultimate block, followed by the full final block. This is not convenient for the receiver for two reasons:
- The receiver must decrypt the final block first in any case, and
- This results in the final block not being aligned on a natural boundary, complicating hardware implementations.
This does have the advantage that, if the final plaintext block happens to be a multiple of the block size, the ciphertext is identical to that of the original mode of operation without ciphertext stealing.
CS2
It is often more convenient to swap the final two ciphertext blocks, so the ciphertext ends with the full final block, followed by the truncated penultimate block. This results in naturally aligned ciphertext blocks.
In order to maintain compatibility with the non-stealing modes, option CS2 performs this swap only if the amount of stolen ciphertext is non-zero, i.e. the original message was not a multiple of the block size.
This maintains natural alignment, and compatibility with the non-stealing modes, but requires treating the cases of aligned and unaligned message size differently.
CS3
The most popular alternative swaps the final two ciphertext blocks unconditionally. This is the ordering used in the descriptions below.
Ciphertext stealing mode description
In order to encrypt or decrypt data, use the standard block cipher mode of operation on all but the last two blocks of data.
The following steps describe how to handle the last two blocks of the plaintext, called Pn−1 and Pn, where the length of Pn−1 equals the block size of the cipher in bits, B; the length of the last block, Pn, is M bits; and K is the key that is in use. M can range from 1 to B, inclusive, so Pn could possibly be a complete block. The CBC mode description also makes use of the ciphertext block just previous to the blocks concerned, Cn−2, which may in fact be the IV if the plaintext fits within two blocks.
For this description, the following functions and operators are used:
- Head (data, a): returns the first a bits of the 'data' string.
- Tail (data, a): returns the last a bits of the 'data' string.
- Encrypt (K, data): use the underlying block cipher in encrypt mode on the 'data' string using the key K.
- Decrypt (K, data): use the underlying block cipher in decrypt mode on the 'data' string using the key K.
- XOR: Bitwise Exclusive-OR. Equivalent to bitwise addition without use of a carry bit.
- ||: Concatenation operator. Combine the strings on either side of the operator.
- 0a: a string of a 0 bits.
ECB ciphertext stealing
Ciphertext stealing in ECB mode introduces an inter-block dependency within the last two blocks, resulting in altered error propagation behavior for the last two blocks.
ECB encryption steps (see figure)
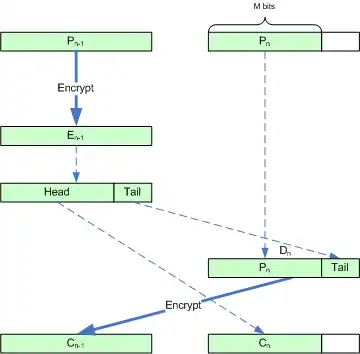
- En−1 = Encrypt (K, Pn−1). Encrypt Pn−1 to create En−1. This is equivalent to the behavior of standard ECB mode.
- Cn = Head (En−1, M). Select the first M bits of En−1 to create Cn. The final ciphertext block, Cn, is composed of the leading M bits of the second-to-last ciphertext block. In all cases, the last two blocks are sent in a different order than the corresponding plaintext blocks.
- Dn = Pn || Tail (En−1, B−M). Pad Pn with the low order bits from En−1.
- Cn−1 = Encrypt (K, Dn). Encrypt Dn to create Cn−1. For the first M bits, this is equivalent to what would happen in ECB mode (other than the ciphertext ordering). For the last B−M bits, this is the second time that these data have been encrypted under this key (It was already encrypted in the production of En−1 in step 2).
ECB decryption steps
- Dn = Decrypt (K, Cn−1). Decrypt Cn−1 to create Dn. This undoes step 4 of the encryption process.
- En−1 = Cn || Tail (Dn, B−M). Pad Cn with the extracted ciphertext in the tail end of Dn (placed there in step 3 of the ECB encryption process).
- Pn = Head (Dn, M). Select the first M bits of Dn to create Pn. As described in step 3 of the ECB encryption process, the first M bits of Dn contain Pn. We queue this last (possibly partial) block for eventual output.
- Pn−1 = Decrypt (K, En−1). Decrypt En−1 to create Pn−1. This reverses encryption step 1.
ECB ciphertext stealing error propagation
A bit error in the transmission of Cn−1 would result in the block-wide corruption of both Pn−1 and Pn. A bit error in the transmission of Cn would result in the block-wide corruption of Pn−1. This is a significant change from ECB's error propagation behavior.
CBC ciphertext stealing
In CBC, there is already interaction between processing of different adjacent blocks, so CTS has less conceptual impact in this mode. Error propagation is affected.
CBC encryption steps
- Xn−1 = Pn−1 XOR Cn−2. Exclusive-OR Pn−1 with the previous ciphertext block, Cn−2, to create Xn−1. This is equivalent to the behavior of standard CBC mode.
- En−1 = Encrypt (K, Xn−1). Encrypt Xn−1 to create En−1. This is equivalent to the behavior of standard CBC mode.
- Cn = Head (En−1, M). Select the first M bits of En−1 to create Cn. The final ciphertext block, Cn, is composed of the leading M bits of the second-to-last ciphertext block. In all cases, the last two blocks are sent in a different order than the corresponding plaintext blocks.
- P = Pn || 0B−M. Pad Pn with zeros at the end to create P of length B. The zero padding in this step is important for step 5.
- Dn = En−1 XOR P. Exclusive-OR En−1 with P to create Dn. For the first M bits of the block, this is equivalent to CBC mode; the first M bits of the previous block's ciphertext, En−1, are XORed with the M bits of plaintext of the last plaintext block. The zero padding of P in step 4 was important, because it makes the XOR operation's effect on the last B−M bits equivalent to copying the last B−M bits of En−1 to the end of Dn. These are the same bits that were stripped off of En−1 in step 3 when Cn was created.
- Cn−1 = Encrypt (K, Dn). Encrypt Dn to create Cn−1. For the first M bits, this is equivalent to what would happen in CBC mode (other than the ciphertext ordering). For the last B−M bits, this is the second time that these data have been encrypted under this key (It was already encrypted in the production of En−1 in step 2).
CBC decryption steps
- Dn = Decrypt (K, Cn−1). Decrypt Cn−1 to create Dn. This undoes step 6 of the encryption process.
- C = Cn || 0B−M. Pad Cn with zeros at the end to create a block C of length B. We are padding Cn with zeros to help in step 3.
- Xn = Dn XOR C. Exclusive-OR Dn with C to create Xn. Looking at the first M bits, this step has the result of XORing Cn (the first M bits of the encryption process' En−1) with the (now decrypted) Pn XOR Head (En−1, M) (see steps 4-5 of the encryption process). In other words, we have CBC decrypted the first M bits of Pn. Looking at the last B−M bits, this recovers the last B−M bits of En−1.
- Pn = Head (Xn, M). Select the first M bits of Xn to create Pn. As described in step 3, the first M bits of Xn contain Pn. We queue this last (possibly partial) block for eventual output.
- En−1 = Cn || Tail (Xn, B−M). Append the tail (B−M) bits of Xn to Cn to create En−1. As described in step 3, En−1 is composed of all of Cn (which is M bits long) appended with the last B−M bits of Xn. We reassemble En−1 (which is the same En−1 seen in the encryption process) for processing in step 6.
- Xn−1 = Decrypt (K, En−1). Decrypt En−1 to create Xn−1. This reverses encryption step 2. Xn−1 is the same as in the encryption process.
- Pn−1 = Xn−1 XOR Cn−2. Exclusive-OR Xn−1 with the previous ciphertext block, Cn−2, to create Pn−1. Finally, we reverse the XOR step from step 1 of the encryption process.
CBC implementation notes
For CBC ciphertext stealing, there is a clever (but opaque) method of implementing the described ciphertext stealing process using a standard CBC interface. Using this method imposes a performance penalty in the decryption stage of one extra block decryption operation over what would be necessary using a dedicated implementation.
CBC ciphertext stealing encryption using a standard CBC interface
- Pad the last partial plaintext block with 0.
- Encrypt the whole padded plaintext using the standard CBC mode.
- Swap the last two ciphertext blocks.
- Truncate the ciphertext to the length of the original plaintext.
_on_CBC%252C_encryption_mode.svg.png.webp)
CBC ciphertext stealing decryption using a standard CBC interface
- Dn = Decrypt (K, Cn−1). Decrypt the second-to-last ciphertext block using ECB mode.
- Cn = Cn || Tail (Dn, B−M). Pad the ciphertext to the nearest multiple of the block size using the last B−M bits of block cipher decryption of the second-to-last ciphertext block.
- Swap the last two ciphertext blocks.
- Decrypt the (modified) ciphertext using the standard CBC mode.
- Truncate the plaintext to the length of the original ciphertext.
_on_CBC%252C_decryption_mode.svg.png.webp)
CBC ciphertext stealing error propagation
A bit error in the transmission of Cn−1 would result in the block-wide corruption of both Pn−1 and Pn. A bit error in the transmission of Cn would result in a corresponding bit error in Pn, and in the block-wide corruption of Pn−1.
References
- Daemen, Joan (1995). "2.5.1 and 2.5.2". Cipher and Hash Function Design, Strategies Based on Linear and Differential Cryptanalysis (PDF) (Ph.D. thesis). Katholieke Universiteit Leuven.
- Schneier, Bruce (1995). Applied Cryptography (2nd ed.). John Wiley & Sons, Inc. pp. 191, 195. ISBN 978-0-471-12845-8.
- Meyer, Carl H.; Matyas, Stephen M. (1982). Cryptography: A New Dimension in Computer Data Security. John Wiley & Sons, Inc. pp. 77–85. ISBN 978-0-471-04892-3.
- R. Baldwin; R. Rivest (October 1996). The RC5, RC5-CBC, RC5-CBC-Pad, and RC5-CTS Algorithms. doi:10.17487/RFC2040. RFC 2040.
- Dworkin, Morris (October 2011). Recommendation for Block Cipher Modes of Operation: Three Variants of Ciphertext Stealing for CBC Mode (PDF). US National Institute of Standards and Technology (NIST). Addendum to NIST Special Pub 800-38A.