Ōno's lexical law, or simply Ōno's law, is a statistical law for the varying rate that four word classes that appear in the lexicon of classical Japanese literary works. The law was discovered by Japanese linguist Susumu Ōno and published in 1956.[1]
Summary
The law states that, for the nine literary works under consideration (one work is in two editions, hence ten manuscripts total), the percentage of words in each of the four given word classes vary simultaneously linearly, between the most noun-heavy Man'yōshū and the most verb-heavy Tale of Genji. The four word classes are nouns, verbs, adjectives, and adjectival nouns, with nouns and verbs being the bulk of the words. If there were only two word classes, this statement would be trivial: as one word class (say, nouns) decreases, the other (say, verbs) increases by exactly the corresponding amount. However, what the law observes is that as use of nouns decreases, use of verbs and adjectives and adjectival nouns increases, and that these increase by approximately constant proportions (hence linear).
The horizontal axis (in Ōno's formulation) is arbitrary, and should not be interpreted as time. The graph in the re-formulation by Mizutani is more easily interpreted, and shows a scatter plot of nouns versus other word classes.
Ōno's lexical law (original version)
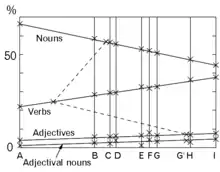
Obtain the rates of usage for four word classes: nouns, verbs, adjectives, and adjectival noun for Man'yōshū and Genji Monogatari. Plot the rates of the four word classes for the Man'yōshū on the y-axis. Then plot the rates for the Genji Monogatari on a vertical line to the right. Connecting the two points for the noun reveals a monotonically decreasing line, while connecting the two points for any of the other word classes results in a monotonically increasing line. Plot an additional point corresponding to any of the other seven classic works on each line of the word classes. This reveals that any of those new point sets for one of the additional works on different lines of word classes is located approximately on a different vertical line.[1]
| Symbols | Literatures |
|---|---|
| A | Man'yōshū |
| B | Tsurezuregusa |
| C | Hōjōki |
| D | Makura no sōshi |
| E | Tosa nikki |
| F | Murasaki Shikibu Nikki |
| G | Sanuki no Suke Nikki |
| G' | Sanuki no Suke Nikki (earlier data before revision) |
| H | Taketori monogatari |
| I | Genji Monogatari |
Revised Ōno's lexical law by Mizutani
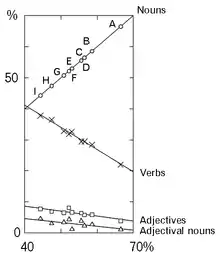
Let the rates of noun usage in the lexicon of 3 arbitrary literary works A, B, and C be , respectively. With rates for usage of another word class of the same 3 literatures, respectively, then 3 points, will approximately be located on a line. Namely,[3][4][5]
| . |
References and notes
- 1 2 Susumu Ōno (1956) A study of several themes on the basic lexicon --In Japanese classical literary works. Kokugogaku (Japanese language) 24: 34–46 (in Japanese)
- ↑ The line of a word class is determined by the two points of Man'yōshū and Genji Monogatari and called a word class line. Then let ai be the x-coordinate of a vertical line corresponding to another literary work i. Define S to be the sum of squares of the difference between the actual rate yi and a y-coordinate of the node of a word class line and the vertical line for a literary work i. S=sum of (yi-yi)^2 for all i (i=1,...,7). S was expressed in the cell of Microsoft Excel sheet and ai was manually changed on the same Excel sheet. In the present case, it was predicted that S would have a local minimal value where Sj>=Si<=Sk if aj<ai<ak. For literary works B, C, ..., H, ai was 38, 46, 49, 62, 66, 70, and 87, respectively. ai was only changed in 1(%) interval for the sake of simplicity.
- ↑ Shizuo Mizutani (1965) On Ōno's lexical law. Keiryo-Kokugogaku (Mathematical Linguistics of Japanese) 35: 1–12. (in Japanese)
- ↑ Shizuo Mizutani (1982) Mathematical Linguistics (Lectures on modern mathematics D-3) Baifukan Publisher, 204pp. (in Japanese)
- ↑ Shizuo Mizutani (1989) Ōno's lexical law: its data adjustment by linear regression. In "Quantitative Linguistics Vol. 39, Japanese Quantitative Linguistics" (ed. Shizuo Mizutani) pp. 1–13, Bochum: Studienverlag Dr. N. Brockmeyer.